Understanding Critical Values in Confidence Intervals
A critical value is a point on the scale of the test statistic beyond which we reject the null hypothesis. It's derived from the chosen confidence level and the sampling distribution of the test statistic. For a 98% confidence interval, the critical value helps define the boundaries within which we expect the true population parameter to lie with 98% certainty.
The Significance of Confidence Levels
The confidence level represents the long-run proportion of confidence intervals that contain the true population parameter. A 98% confidence level signifies that if we were to construct numerous confidence intervals from repeated samples, approximately 98% of those intervals would contain the true population parameter. The remaining 2% represents the significance level (alpha, α), which is the probability of rejecting a true null hypothesis (Type I error).
Calculating the Critical Value for a 98% Confidence Interval
The method for calculating the critical value depends on the sampling distribution and whether it's a one-tailed or two-tailed test. For confidence intervals, we generally use two-tailed tests because we're interested in estimating a range of plausible values for the parameter, rather than testing whether it's greater than or less than a specific value.
Using the Z-Distribution (Normal Distribution)
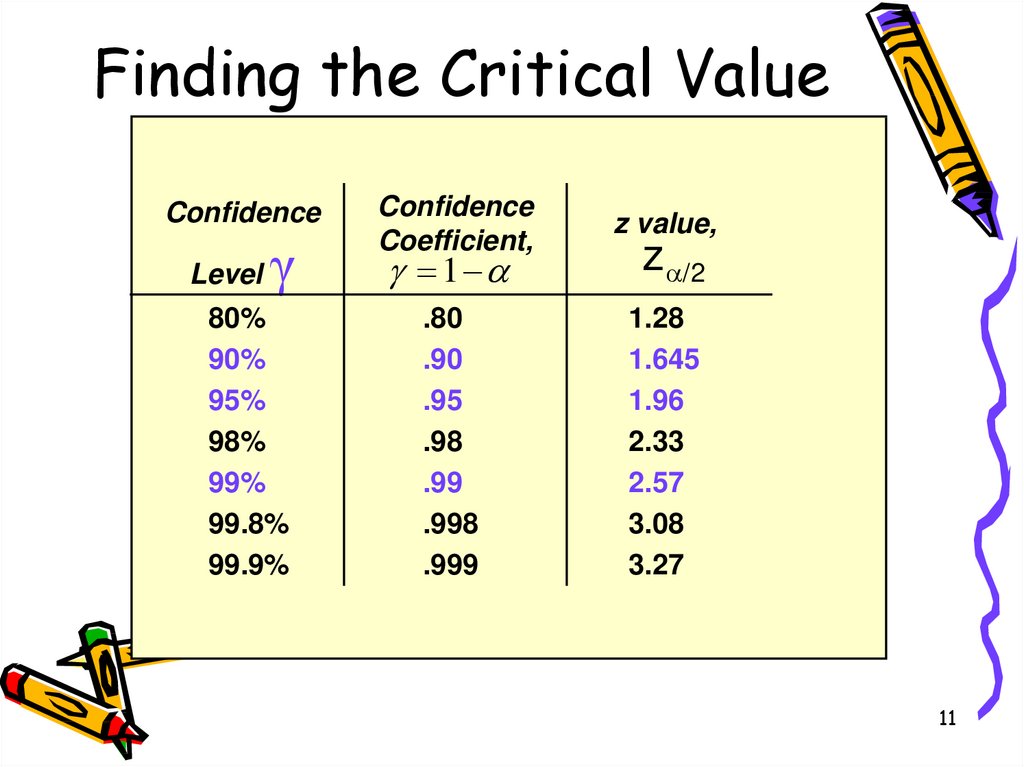
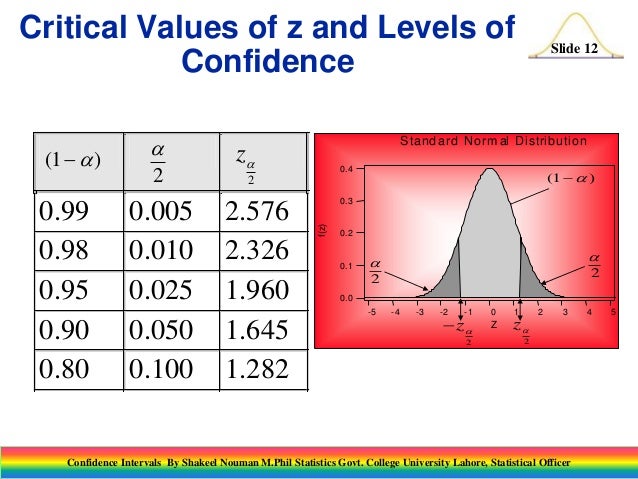
When the population standard deviation is known or the sample size is sufficiently large (typically n > 30), the Z-distribution (standard normal distribution) is used. To find the critical value (Z-critical) for a 98% confidence interval, we need to find the Z-score that corresponds to the remaining area in the tails of the distribution.
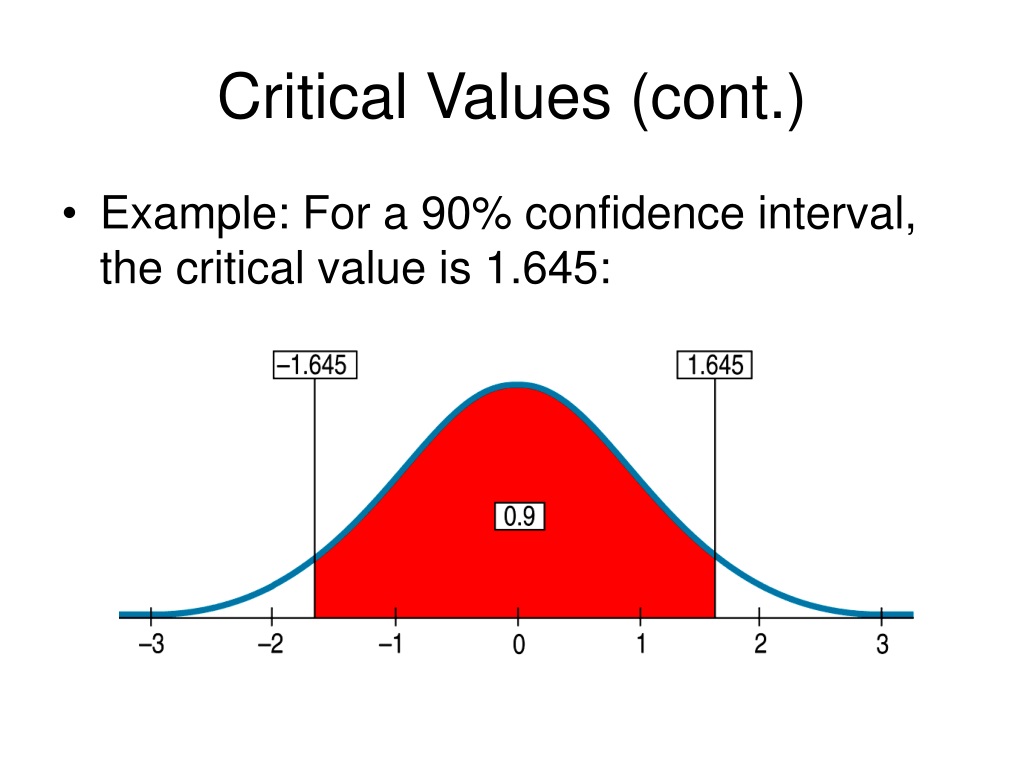
Since it's a two-tailed test, the alpha (α) is divided by 2 (α/2). For a 98% confidence level, α = 1 - 0.98 = 0.02. Therefore, α/2 = 0.01. This means we need to find the Z-score that leaves 0.01 in the upper tail of the standard normal distribution.
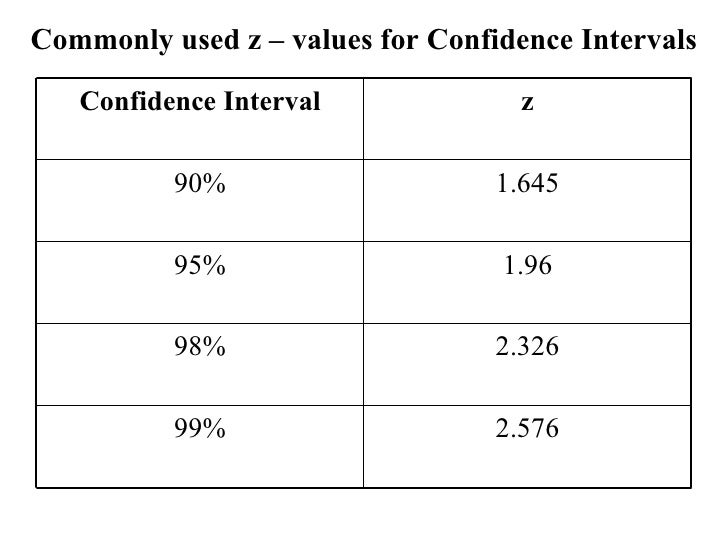
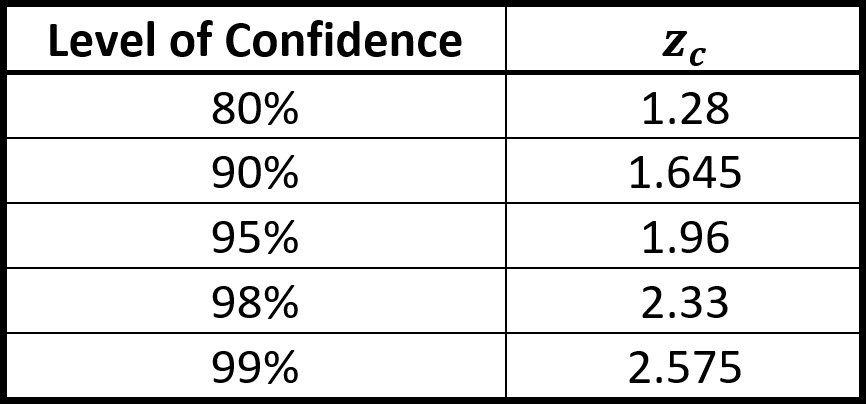
This can be done using a Z-table (standard normal table), a statistical calculator, or software. Looking up the Z-score corresponding to a cumulative probability of 1 - 0.01 = 0.99 in a Z-table yields a Z-critical value of approximately 2.33.
Therefore, for a 98% confidence interval using the Z-distribution, the critical value is approximately 2.33.
Example: If you are constructing a 98% confidence interval for the population mean based on a sample with a known population standard deviation, the critical value you would use is 2.33.
Using the T-Distribution
When the population standard deviation is unknown and estimated by the sample standard deviation, and the sample size is small (typically n ≤ 30), the T-distribution is used. The T-distribution is similar to the Z-distribution but has heavier tails, reflecting the added uncertainty from estimating the standard deviation. The T-distribution's shape depends on the degrees of freedom (df), which is calculated as n - 1, where n is the sample size.
To find the critical value (T-critical) for a 98% confidence interval using the T-distribution, we need to know the degrees of freedom (df) and the α/2 value (0.01, as calculated previously). We then consult a T-table or use statistical software to find the T-critical value.
Important Considerations for T-Distribution:
- The T-critical value will be larger than the Z-critical value for the same confidence level, especially for small sample sizes.
- As the sample size (and therefore the degrees of freedom) increases, the T-distribution approaches the Z-distribution, and the T-critical value approaches the Z-critical value.
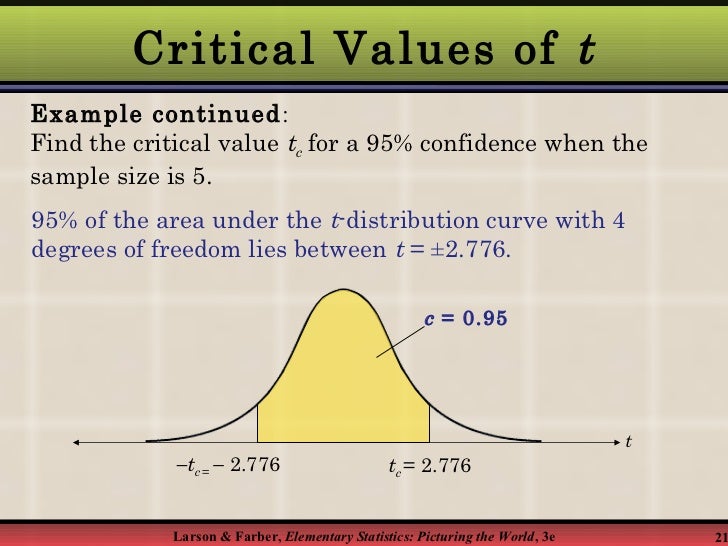
Example: Suppose you are constructing a 98% confidence interval for the population mean based on a sample of size 15. The degrees of freedom would be 15 - 1 = 14. Using a T-table with 14 degrees of freedom and α/2 = 0.01, the T-critical value would be approximately 2.624.
Formula for Confidence Interval Calculation
The general formula for a confidence interval is:
Sample Statistic ± (Critical Value * Standard Error)
Where:
- Sample Statistic is the point estimate of the population parameter (e.g., sample mean).
- Critical Value is the Z-critical or T-critical value, depending on the distribution used.
- Standard Error is the standard deviation of the sample statistic.
Example using Z-distribution: If the sample mean is 50, the population standard deviation is 10, and the sample size is 100, then the standard error is 10/√100 = 1. Using a Z-critical value of 2.33, the 98% confidence interval would be:
50 ± (2.33 * 1) = 50 ± 2.33
Therefore, the confidence interval is (47.67, 52.33).
Example using T-distribution: If the sample mean is 50, the sample standard deviation is 10, and the sample size is 15, then the standard error is 10/√15 ≈ 2.58. The degrees of freedom is 14, and the T-critical value is approximately 2.624. The 98% confidence interval would be:
50 ± (2.624 * 2.58) ≈ 50 ± 6.77
Therefore, the confidence interval is approximately (43.23, 56.77).
Interpreting the 98% Confidence Interval
After calculating the confidence interval, the key is to understand its meaning. We can state that we are 98% confident that the true population parameter (e.g., population mean) lies within the calculated interval. It is crucial to avoid stating that there is a 98% probability that the true population parameter lies within the interval. The parameter is a fixed value, and the interval is what varies from sample to sample.
Factors Affecting Confidence Interval Width
Several factors influence the width of a confidence interval:
- Confidence Level: A higher confidence level (e.g., 99%) results in a wider interval, reflecting the increased certainty required.
- Sample Size: A larger sample size results in a narrower interval, as the estimate becomes more precise.
- Standard Deviation: A larger standard deviation results in a wider interval, as there is more variability in the data.
Practical Applications
Confidence intervals are widely used in various fields:
- Market Research: Estimating the proportion of customers who prefer a particular product.
- Healthcare: Determining the effectiveness of a new treatment.
- Finance: Assessing the range of plausible returns for an investment.
- Quality Control: Monitoring the consistency of a manufacturing process.
Conclusion
Understanding the critical value for a 98% confidence interval is crucial for accurately estimating population parameters and making informed decisions based on sample data. The choice between the Z-distribution and T-distribution depends on whether the population standard deviation is known and the sample size. A larger sample size will yield a more precise (narrower) confidence interval. It’s important to correctly interpret the confidence interval, stating that we are 98% confident that the true population parameter lies within the interval. Key takeaways:
- For a 98% confidence interval using the Z-distribution, the critical value is approximately 2.33.
- For a 98% confidence interval using the T-distribution, the critical value depends on the degrees of freedom (n-1) and is typically found using a T-table or statistical software.
- The confidence interval formula is: Sample Statistic ± (Critical Value * Standard Error).
- A 98% confidence interval means we are 98% confident that the true population parameter lies within the calculated interval.