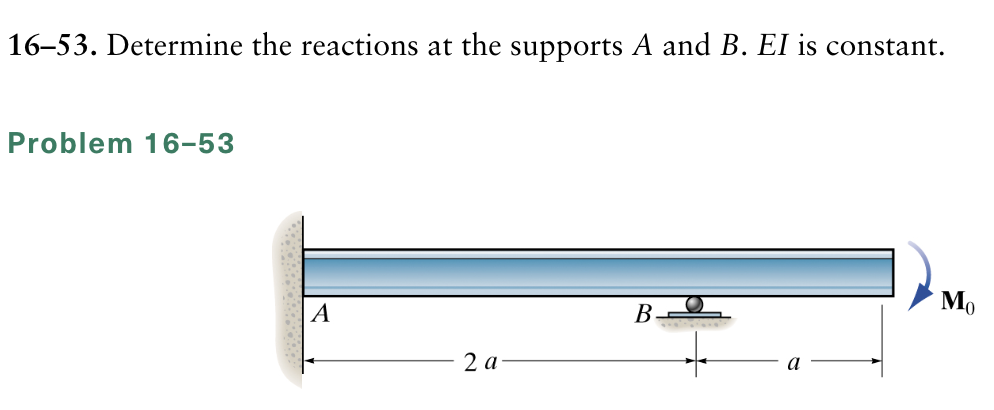
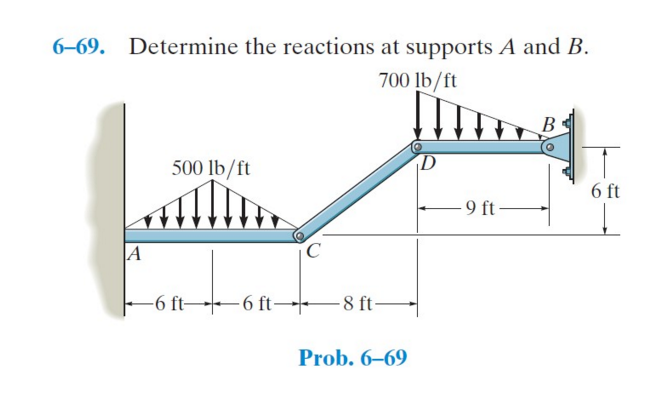
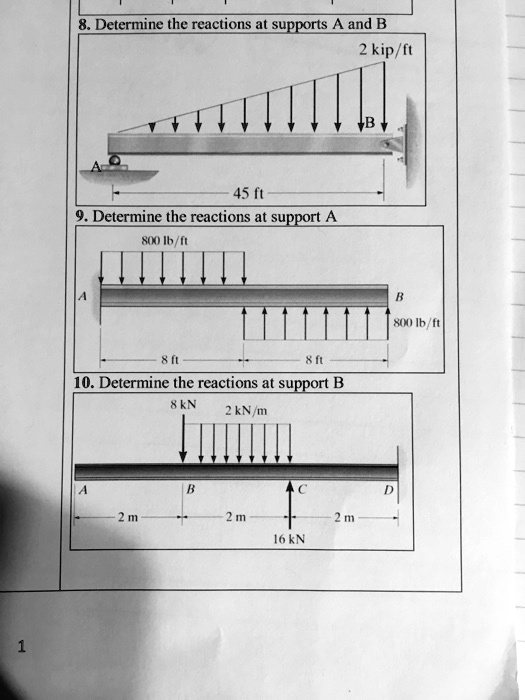
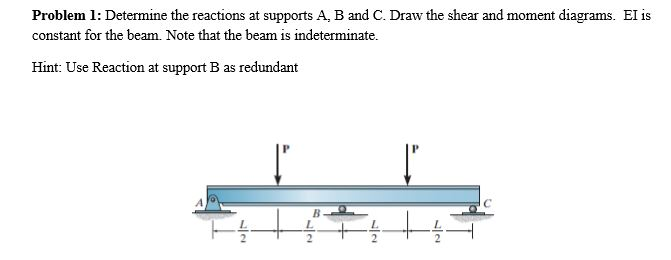
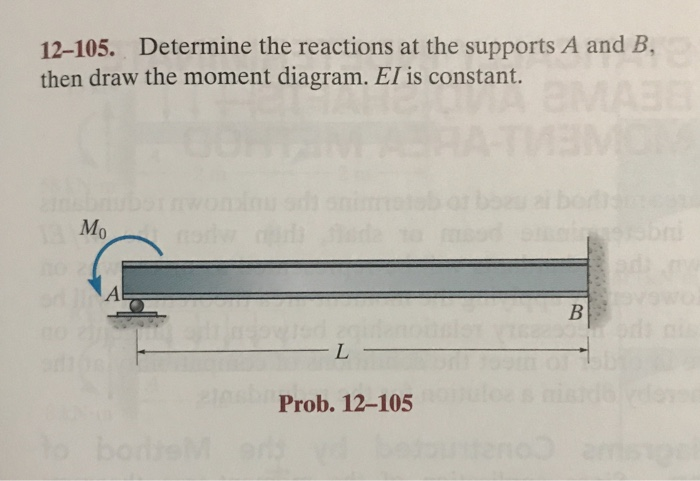
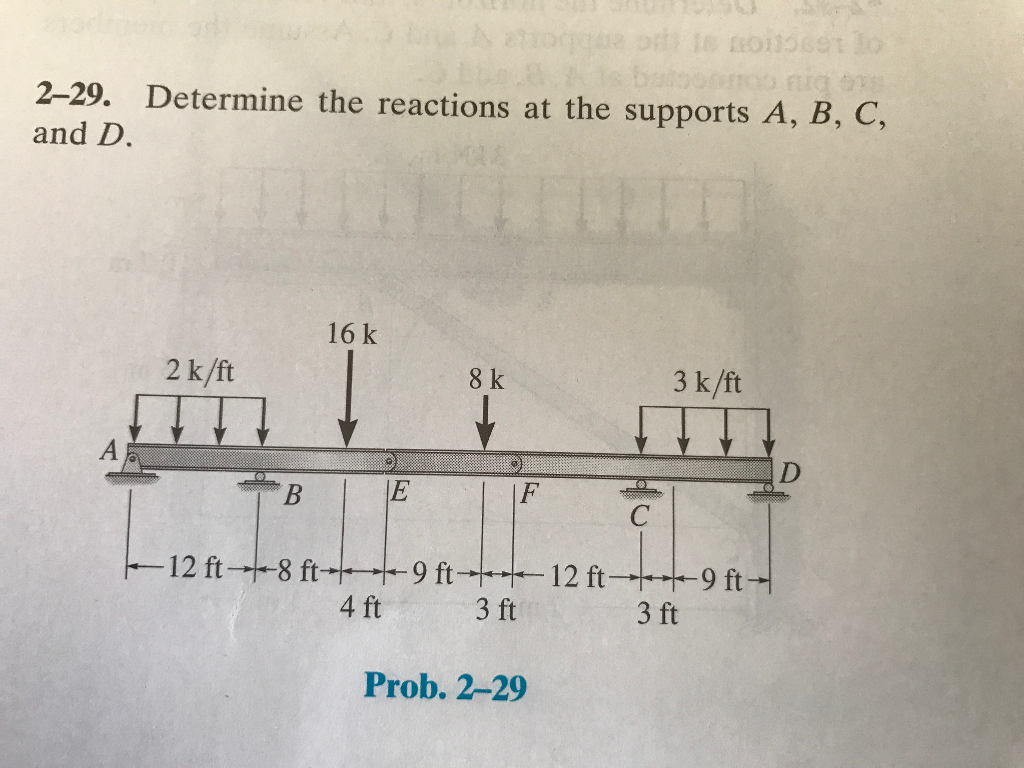
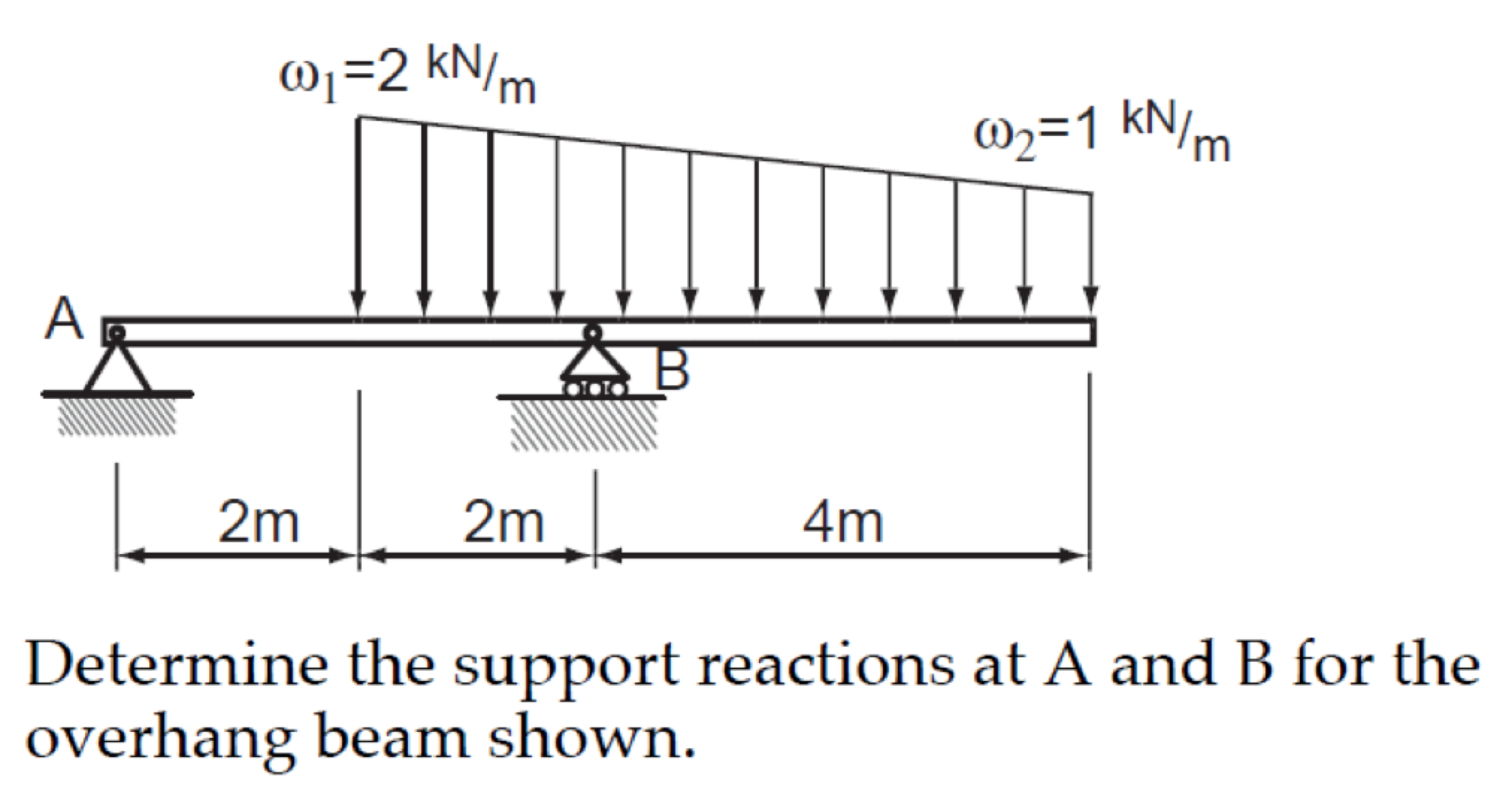
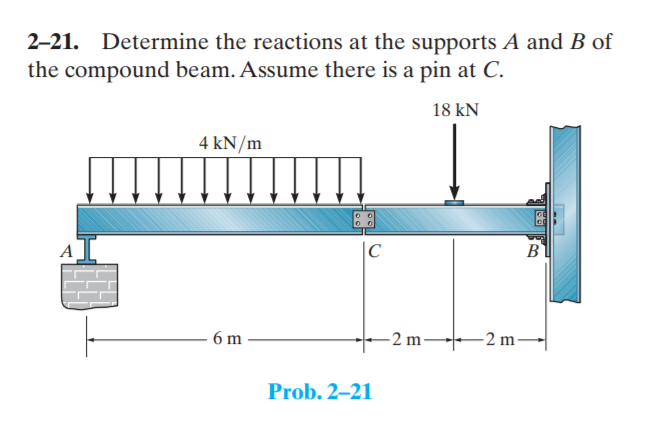
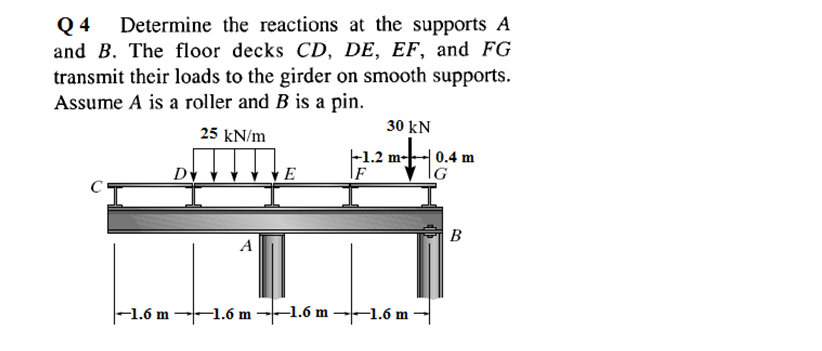
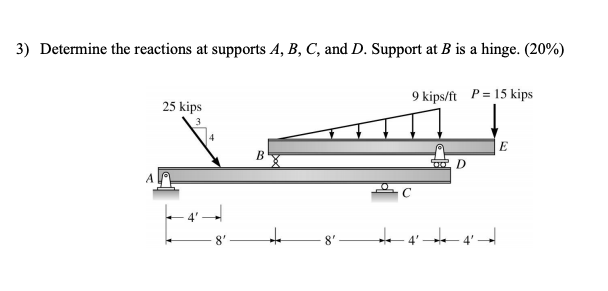
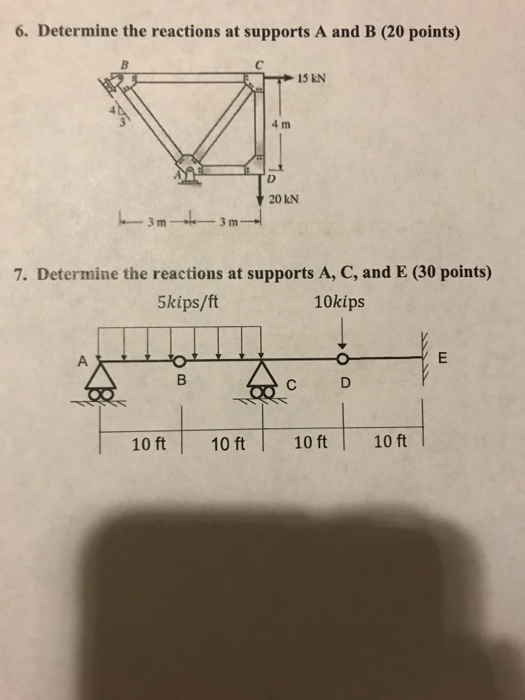
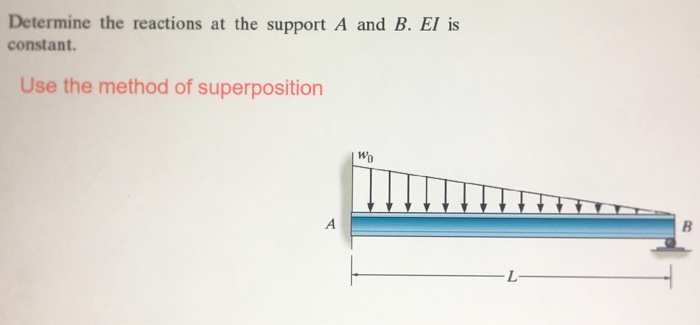
Let's talk about how to determine the reactions at supports in structures. This isn't just theoretical; it's something that comes up frequently in real-world scenarios, whether you're dealing with a simple shelf or a more complex building design.
Understanding Support Reactions
Support reactions are the forces exerted by supports on a structure to keep it in equilibrium. Identifying these reactions is a fundamental step in structural analysis, enabling you to determine internal forces and stresses within the structure. This directly translates to ensuring safety and stability in designs.
Free Body Diagrams: Your Visual Aid
The first step is always to draw a free body diagram (FBD). This is a simplified representation of the structure showing all external forces acting on it, including applied loads and support reactions. Represent each support with its appropriate reaction components. For example:
- Pin Support: Two reaction components – a vertical force (Ay) and a horizontal force (Ax).
- Roller Support: One reaction component – a vertical force (By) perpendicular to the surface.
- Fixed Support: Three reaction components – a vertical force (Ay), a horizontal force (Ax), and a moment (Ma).
Clearly label all forces and distances on your FBD. A messy or incomplete diagram will lead to errors.
Equations of Equilibrium: The Foundation
To solve for the unknown support reactions, you'll use the equations of static equilibrium. These equations state that for a structure to be in equilibrium, the sum of all forces and moments acting on it must be zero.
- ΣFx = 0: The sum of all horizontal forces must equal zero.
- ΣFy = 0: The sum of all vertical forces must equal zero.
- ΣM = 0: The sum of all moments about any point must equal zero.
Apply these equations to your FBD. Choose a point strategically for your moment equation. Picking a point where several unknown forces intersect will simplify the equation by eliminating those unknowns.
Solving for the Unknowns: The Math
Now you have a system of equations. The number of equations must be equal to or greater than the number of unknown support reactions to solve the system statically. Solve these equations simultaneously to determine the values of the unknown reactions.
Important Tip: If you assume a direction for a reaction component and solve for a negative value, it simply means the actual direction is opposite to your initial assumption. Don't change the sign in your other equations; just be aware of the actual direction.
Applying This Knowledge in Daily Life and Work
This isn't just for structural engineers. The principles of support reactions are relevant in many everyday situations:
- Hanging a Picture: When you hang a picture, the nail acts as a support. Understanding the load (weight of the picture) helps you choose a nail strong enough to provide the necessary reaction. If the picture is hanging by two nails, the load is distributed, and each nail needs to provide a smaller reaction.
- Loading a Shelf: Consider the weight distribution on a shelf. If you place heavy objects in the center, the supports (brackets or shelf standards) at either end need to provide significant vertical reactions. Placing heavier items closer to the supports reduces the bending moment on the shelf and distributes the load more effectively.
- Furniture Assembly: When assembling furniture, understanding where the loads are concentrated and how the supports are designed is critical. Overloading a single point or neglecting proper support can lead to structural failure.
- Home Renovations: Planning to remove or modify a wall? Understanding the wall's load-bearing function and the support it provides to the structure above is crucial. Removing a load-bearing wall without proper support can have disastrous consequences.
- Vehicle Loading: When loading a vehicle, distributing the weight evenly is important for stability and to avoid overloading any particular axle or suspension component. The axles and suspension act as supports, providing reactions to the weight of the vehicle and its cargo.
In professional settings, this knowledge is even more critical:
- Construction: Understanding support reactions is fundamental to ensuring the structural integrity of buildings, bridges, and other structures.
- Manufacturing: Designing stable platforms or fixtures for manufacturing processes requires careful consideration of load distribution and support reactions.
- Aerospace: In aircraft design, understanding the reactions at wing supports and landing gear is essential for safe and efficient flight.
Let's look at a practical example. Suppose you are building a simple wooden bridge to cross a small creek in your backyard. The bridge is 10 feet long and supported at both ends. You estimate the maximum load on the bridge will be 500 lbs (yourself and equipment). Assume the supports are simple supports, meaning they offer vertical reaction forces.
1. Free Body Diagram: Draw a line representing the bridge. Mark the two supports (A and B) at each end. Draw a downward arrow representing the 500 lb load. Assuming the load is applied in the center of the bridge (5 feet from each support), mark this location on your diagram.
2. Equations of Equilibrium:
ΣFx = 0 (No horizontal forces, so this equation is trivial)
ΣFy = 0: Ay + By - 500 = 0
ΣMA = 0: (By * 10) - (500 * 5) = 0
3. Solving: From the moment equation, we get By = (500 * 5) / 10 = 250 lbs.
Substituting this into the vertical force equation: Ay + 250 - 500 = 0, so Ay = 250 lbs.
Therefore, each support provides a reaction force of 250 lbs. This means each support needs to be strong enough to handle at least 250 lbs. You would use this information to select appropriate materials for the supports.
Common Mistakes to Avoid
- Incorrect Free Body Diagram: A poorly drawn or incomplete FBD is the most common source of errors. Ensure all forces, moments, and distances are accurately represented.
- Sign Conventions: Be consistent with your sign conventions for forces and moments. Clockwise moments are often considered negative, and counter-clockwise moments positive, but the key is consistency.
- Unit Consistency: Ensure all units are consistent throughout your calculations. Mixing feet and inches, for example, will lead to incorrect results.
- Forgetting Reactions: Don't forget to include all the appropriate reaction components for each type of support.
- Misinterpreting Results: Remember that a negative reaction simply means the assumed direction was incorrect.
Checklist for Determining Support Reactions
Follow this guideline to ensure accurate calculations:
- Draw a clear and complete Free Body Diagram.
- Identify all known and unknown forces and moments.
- Apply the equations of static equilibrium (ΣFx = 0, ΣFy = 0, ΣM = 0).
- Choose a convenient point for calculating moments to simplify equations.
- Solve the system of equations for the unknown support reactions.
- Check your answers for reasonableness and unit consistency.
- Interpret the results correctly, noting the actual direction of any negative reactions.