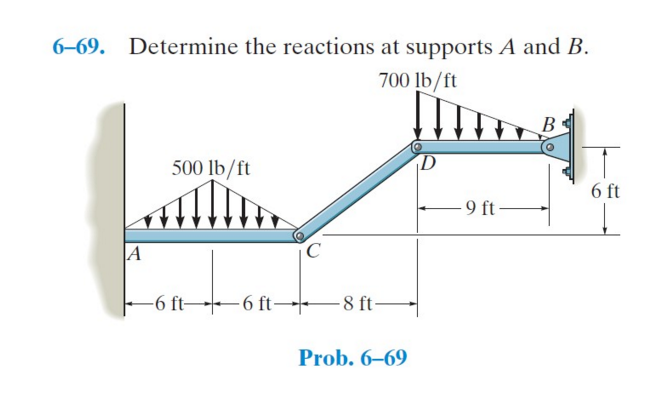
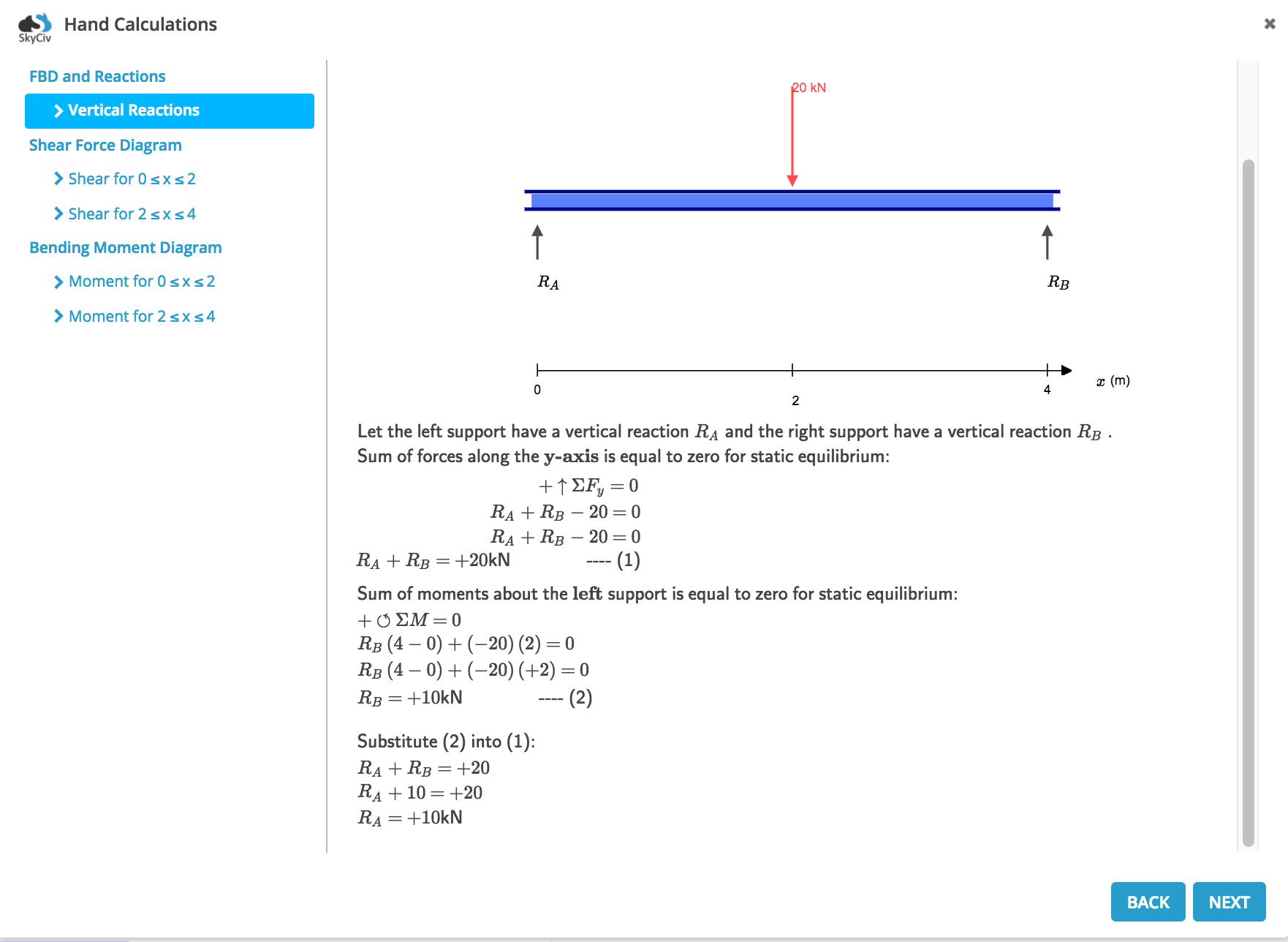
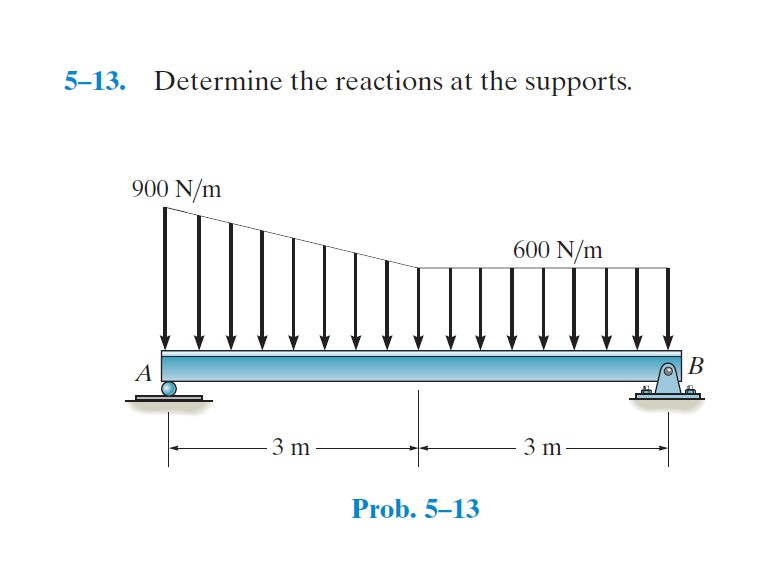
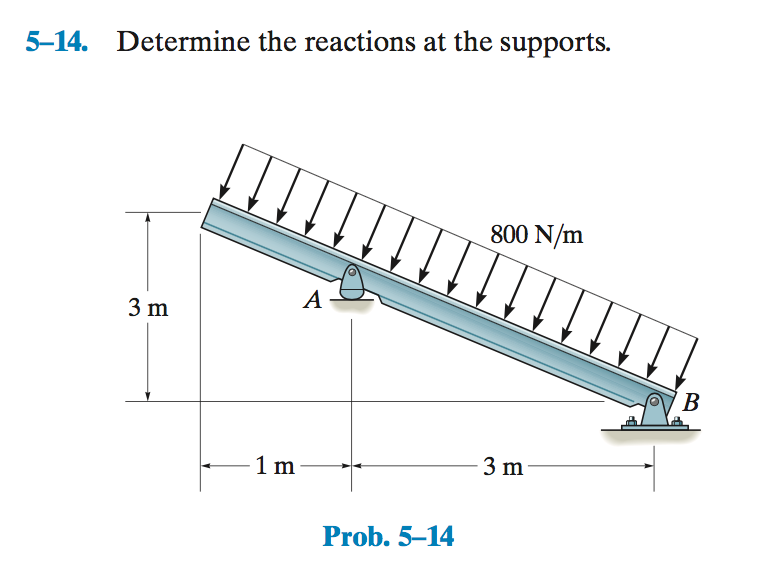
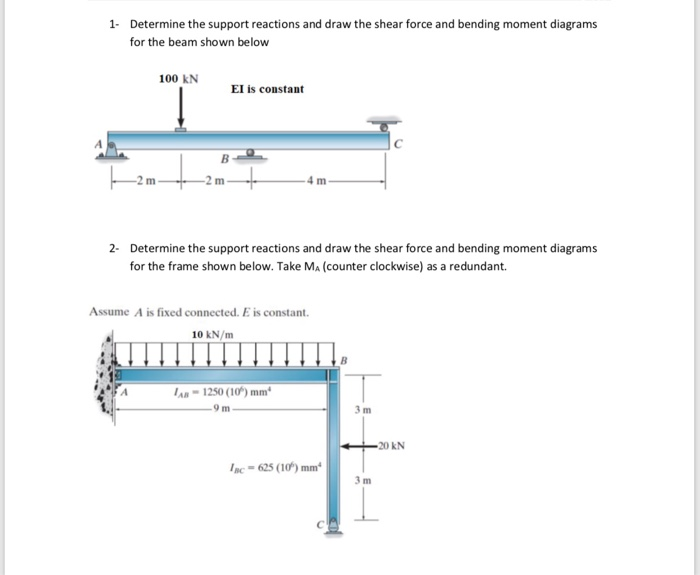
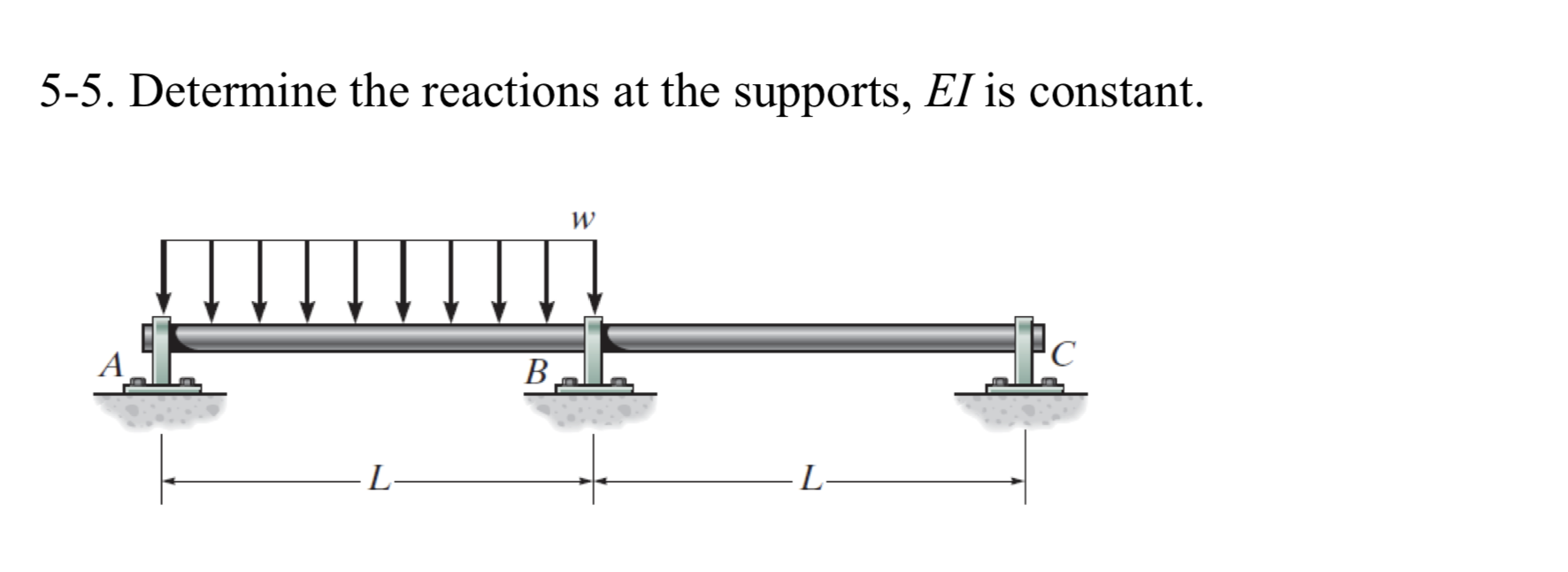
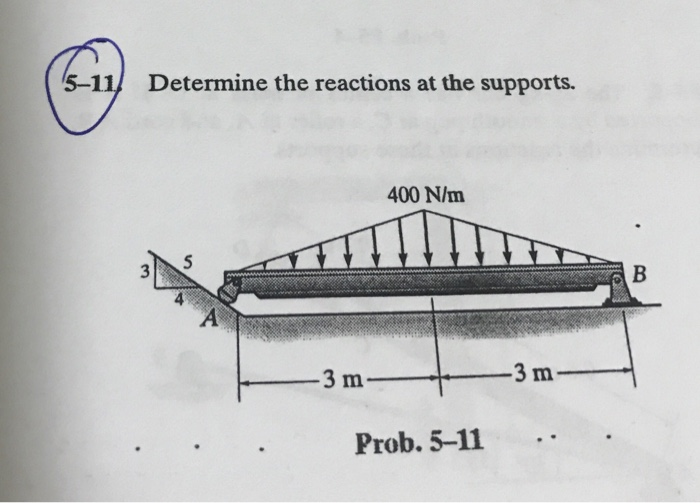
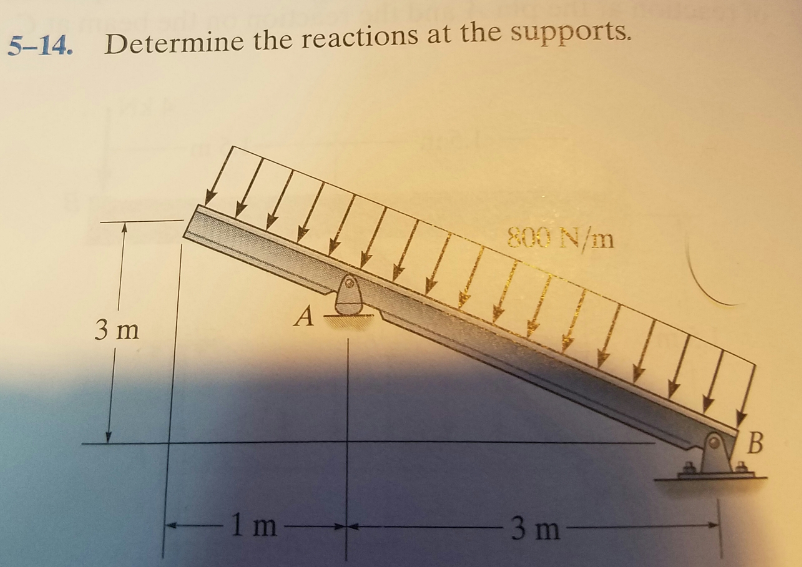
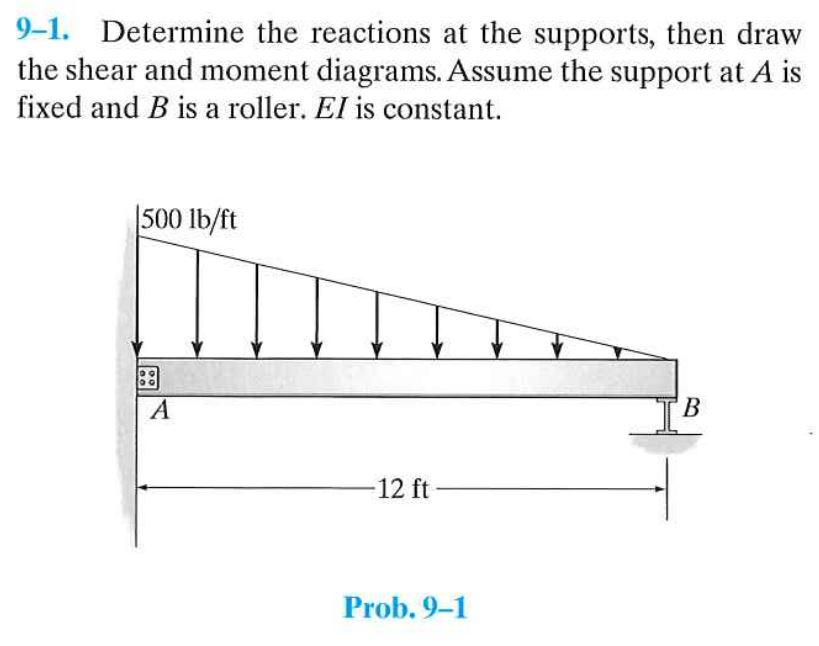
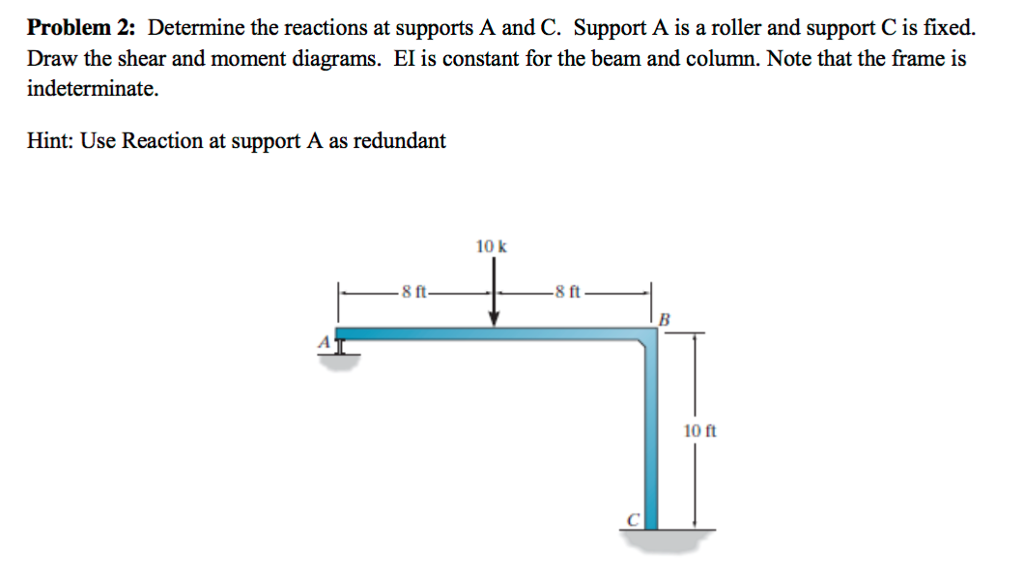
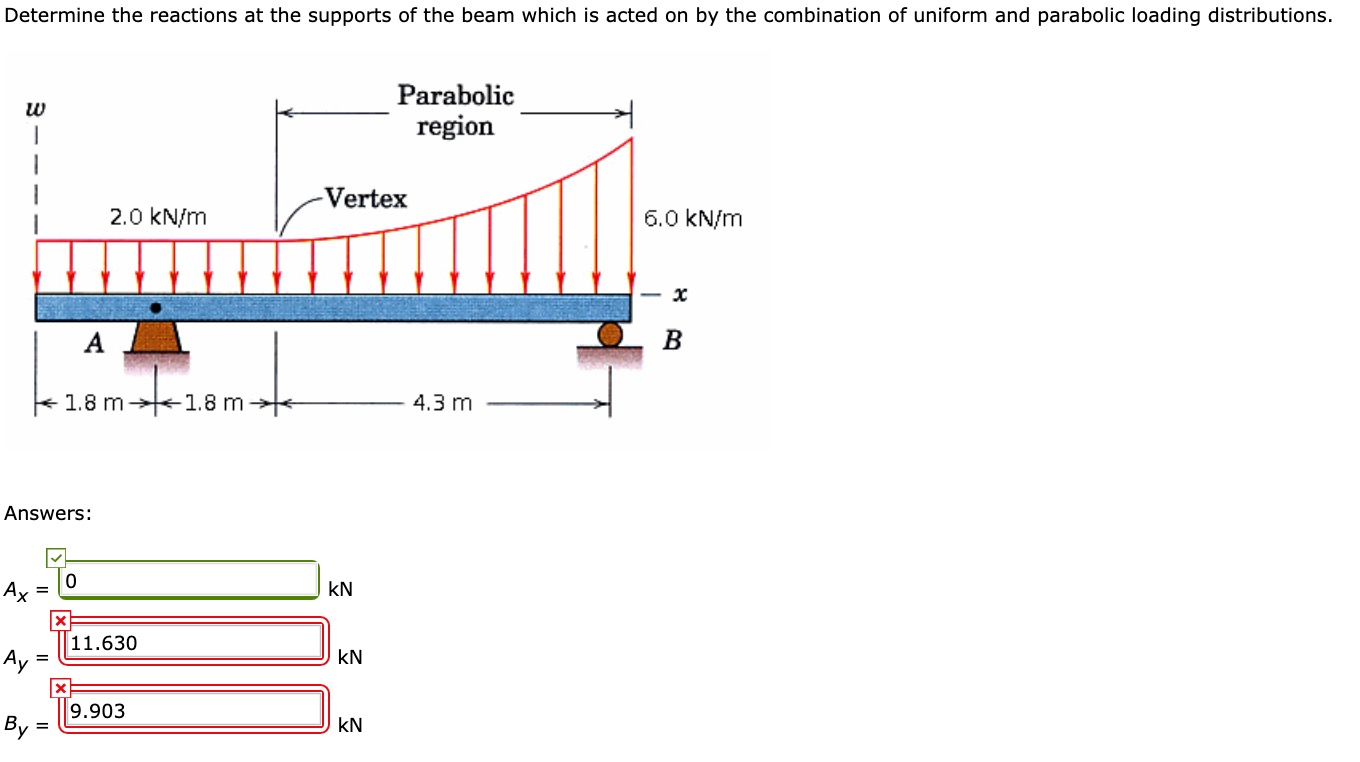
Determining the reactions at the supports of a structure is a fundamental concept in structural mechanics and is crucial for ensuring the stability and safety of any engineered system. It involves calculating the forces and moments exerted by the supports on the structure to counteract the applied loads and maintain equilibrium.
Understanding Supports and Reactions
A support is a structural element that provides resistance to movement. Common types of supports include:
- Roller Supports: These supports allow rotation and translation in one direction, typically horizontally. They provide a vertical reaction force only.
- Hinge Supports (Pin Supports): These supports allow rotation but prevent translation in any direction. They provide both horizontal and vertical reaction forces.
- Fixed Supports (Cantilever Supports): These supports prevent both rotation and translation. They provide both horizontal and vertical reaction forces, as well as a moment reaction.
A reaction is the force or moment exerted by the support on the structure. These reactions are equal in magnitude and opposite in direction to the forces and moments the structure exerts on the support, as dictated by Newton's Third Law of Motion.
The Principles of Equilibrium
The foundation for determining support reactions lies in the principles of static equilibrium. For a structure to be in equilibrium, the following conditions must be satisfied:
- Sum of Forces in the x-direction = 0: ΣFx = 0
- Sum of Forces in the y-direction = 0: ΣFy = 0
- Sum of Moments about any point = 0: ΣM = 0
These equations state that the sum of all external forces acting on the structure in both the horizontal (x) and vertical (y) directions must equal zero, and the sum of all moments about any point must also equal zero. Applying these equations allows us to solve for the unknown support reactions.
Step-by-Step Procedure for Determining Support Reactions
Step 1: Draw a Free Body Diagram (FBD)
The first and most crucial step is to create a clear and accurate Free Body Diagram (FBD) of the structure. This involves:
- Representing the structure as a simplified line diagram.
- Showing all external forces acting on the structure, including applied loads and the weight of the structure itself (if significant).
- Replacing each support with its corresponding reaction forces and moments. Use assumed directions for the unknown reactions; the calculations will reveal the true directions (positive values indicate the assumed direction was correct, negative values indicate the opposite).
Step 2: Apply the Equilibrium Equations
Using the FBD, apply the three equilibrium equations (ΣFx = 0, ΣFy = 0, ΣM = 0) to solve for the unknown reaction forces and moments. The order in which these equations are applied can affect the ease of the solution. Here's a breakdown of common strategies:
Strategy 1: Sum of Moments First
Begin by summing moments about a point where multiple unknown reaction forces intersect. This eliminates those unknowns from the moment equation, allowing you to solve for a single unknown reaction directly. Choose a point strategically to simplify the calculations.
Strategy 2: Sum of Forces
After solving for at least one reaction using the moment equation, apply the force equilibrium equations (ΣFx = 0 and ΣFy = 0) to solve for the remaining unknown reaction forces.
Step 3: Verify the Results
After calculating all the reaction forces and moments, it's essential to verify the results. One method is to sum moments about a different point than the one used initially. If the sum of moments about this new point is equal to zero, it provides confidence in the accuracy of the calculations. Another way is to logically assess whether the calculated reactions make sense given the applied loads and the support conditions.
Example Problem
Consider a simply supported beam with a hinge support at point A and a roller support at point B. The beam has a length of L and is subjected to a vertical point load P at the mid-span (L/2).
- FBD: Draw the beam, indicating the hinge support at A (with reactions Ax and Ay) and the roller support at B (with reaction By). Show the point load P acting downwards at L/2.
- Equilibrium Equations:
- ΣFx = 0: Ax = 0 (since there are no other horizontal forces)
- ΣM_A = 0: By * L - P * (L/2) = 0 => By = P/2
- ΣFy = 0: Ay + By - P = 0 => Ay + (P/2) - P = 0 => Ay = P/2
- Verification: Sum moments about point B: ΣM_B = 0: -Ay * L + P * (L/2) = 0 => -(P/2) * L + P * (L/2) = 0. This confirms the solution.
Therefore, the reactions are: Ax = 0, Ay = P/2 (upwards), and By = P/2 (upwards).
Advanced Considerations
- Distributed Loads: If the beam is subjected to a distributed load (e.g., a uniform load), it needs to be converted into an equivalent point load for the purpose of calculating reactions. The equivalent point load is equal to the total distributed load, and it acts at the centroid of the distributed load.
- Inclined Loads: Inclined loads should be resolved into their horizontal and vertical components before applying the equilibrium equations.
- Statically Indeterminate Structures: Some structures have more unknown reactions than available equilibrium equations. These are called statically indeterminate structures and require additional methods, such as the method of consistent deformations or the slope-deflection method, to solve for the reactions.
Practical Insights
Understanding support reactions is not just an academic exercise; it has practical applications in various everyday situations. For example:
- Home Improvement: When building a deck or installing shelves, understanding the loads and support reactions helps ensure the structure can safely carry the intended weight. Knowing how to properly support a beam or shelf can prevent sagging or collapse.
- Vehicle Loading: When loading items into a vehicle, considering the weight distribution and how it affects the suspension (which acts as a support) is crucial. Overloading one side can lead to instability and damage.
- Understanding Bridges: The design of bridges heavily relies on calculating support reactions to withstand the weight of vehicles, wind loads, and seismic activity. The placement and type of supports are carefully engineered to distribute the loads safely.
In conclusion, determining the reactions at the supports is a fundamental skill in structural analysis. Mastering this skill requires a solid understanding of equilibrium principles, careful application of free body diagrams, and a systematic approach to solving the equilibrium equations. By understanding these concepts, one can ensure the safety and stability of various engineered structures.