Understanding the Period of a Voltage Source
The period of a voltage source is a fundamental characteristic that defines the duration of one complete cycle of its voltage waveform. This is particularly relevant for alternating current (AC) voltage sources, where the voltage fluctuates cyclically over time. For direct current (DC) voltage sources, which ideally provide a constant voltage, the concept of a period is less directly applicable, though variations or ripple in the DC voltage can exhibit a period-like behavior.
Defining the Period
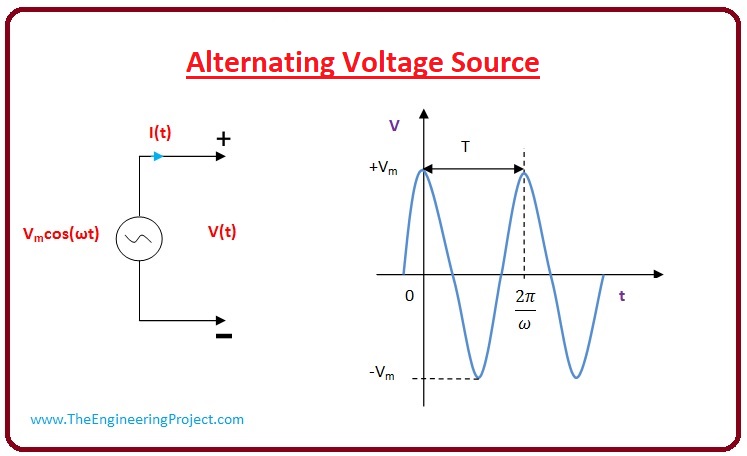
The period (T) is defined as the time it takes for a voltage waveform to repeat itself. It is measured in seconds (s). For a sinusoidal AC voltage source, this represents the time required for the voltage to complete one full sine wave, from its positive peak, through zero, to its negative peak, and back to zero, ending where it started.
Mathematically, the relationship between the period (T) and the frequency (f) of a voltage source is inversely proportional:
T = 1 / f
Where:
- T is the period in seconds.
- f is the frequency in Hertz (Hz), which represents the number of cycles per second.
AC Voltage Sources
The most common example of a periodic voltage source is the AC power supply used in homes and industries. In many countries, the standard frequency is 50 Hz, resulting in a period of 20 milliseconds (0.02 seconds). In North America, the standard frequency is 60 Hz, giving a period of approximately 16.67 milliseconds (0.01667 seconds).
The voltage waveform of an AC source can be represented as:
V(t) = Vpeak * sin(2πft + φ)
Where:
- V(t) is the instantaneous voltage at time t.
- Vpeak is the peak voltage.
- f is the frequency.
- φ is the phase angle.
Understanding the period is crucial for analyzing and designing circuits that operate with AC voltage sources. It directly affects the behavior of components such as capacitors and inductors, whose impedance is frequency-dependent.
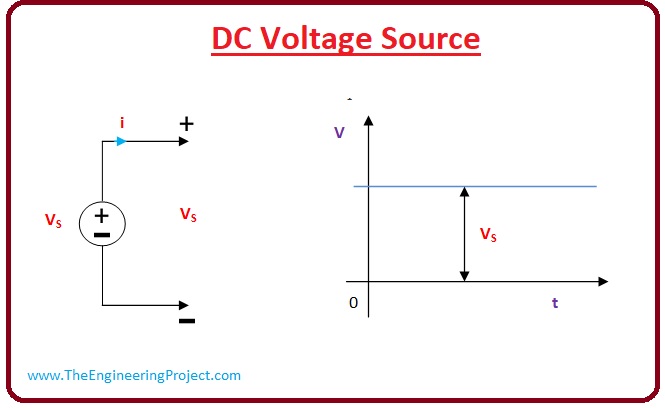
DC Voltage Sources and Ripple
Ideally, a DC voltage source provides a constant voltage over time. Therefore, the period, as strictly defined for AC signals, is not a primary characteristic. However, in practical DC power supplies, there is often some amount of residual AC voltage present, known as ripple voltage. This ripple arises from the imperfect filtering of the AC voltage after rectification.
The ripple voltage typically has a frequency that is related to the AC line frequency (e.g., 50 Hz or 60 Hz) or a multiple thereof (e.g., 100 Hz or 120 Hz for full-wave rectification). The period of this ripple can be calculated in the same way as for AC voltage sources: T = 1/f. However, it’s important to note that the ripple period describes the fluctuation in the DC voltage, not the DC voltage itself.
The magnitude and frequency of the ripple voltage are important parameters for evaluating the quality of a DC power supply. High ripple can negatively impact the performance of sensitive electronic circuits, leading to noise, instability, or even damage.
Impact of Period on Circuit Behavior
The period (or frequency) of a voltage source significantly influences the behavior of circuits, particularly those containing reactive components such as capacitors and inductors.
Capacitors
The impedance of a capacitor is inversely proportional to the frequency of the voltage source:
ZC = 1 / (2πfC)
Where:
- ZC is the impedance of the capacitor.
- f is the frequency of the voltage source.
- C is the capacitance.
This means that a capacitor offers a lower impedance (i.e., less resistance to current flow) at higher frequencies (shorter periods) and a higher impedance at lower frequencies (longer periods). At DC (frequency = 0 Hz), a capacitor ideally acts as an open circuit.
Inductors
The impedance of an inductor is directly proportional to the frequency of the voltage source:
ZL = 2πfL
Where:
- ZL is the impedance of the inductor.
- f is the frequency of the voltage source.
- L is the inductance.
Therefore, an inductor offers a higher impedance at higher frequencies (shorter periods) and a lower impedance at lower frequencies (longer periods). At DC (frequency = 0 Hz), an inductor ideally acts as a short circuit.
Resonance
In circuits containing both capacitors and inductors, resonance can occur. The resonant frequency is the frequency at which the impedances of the capacitor and inductor cancel each other out, leading to a minimum impedance (in a series resonant circuit) or a maximum impedance (in a parallel resonant circuit). The resonant frequency (f0) is given by:
f0 = 1 / (2π√(LC))
Where:
- f0 is the resonant frequency.
- L is the inductance.
- C is the capacitance.
Understanding the period (or frequency) of the voltage source is critical for determining whether a circuit will operate near its resonant frequency, as this can have significant effects on the circuit's behavior, such as increased voltage or current levels.
Measurement of the Period
The period of a voltage source can be measured using several instruments:
- Oscilloscope: An oscilloscope displays the voltage waveform as a function of time, allowing the period to be directly measured from the screen. The time between two corresponding points on consecutive cycles of the waveform (e.g., two positive peaks) represents the period.
- Frequency Counter: A frequency counter measures the frequency of the voltage source. The period can then be calculated using the formula T = 1/f.
- Multimeter: While a standard multimeter primarily measures voltage, current, and resistance, some advanced multimeters include frequency measurement capabilities, allowing the period to be derived.
When measuring the period, it's important to ensure that the instrument is properly calibrated and that the measurement is taken under stable operating conditions.
Applications
Understanding the period of a voltage source is crucial in many applications, including:
- Power Systems: Determining the period of the AC power grid is essential for the design and operation of electrical equipment and systems.
- Electronics Design: The period is critical for designing filters, oscillators, amplifiers, and other electronic circuits.
- Communications: In communication systems, the period of carrier signals and modulation signals plays a crucial role in signal transmission and reception.
- Control Systems: Understanding the period of input signals is important for designing stable and responsive control systems.
Conclusion: Key Takeaways
The period of a voltage source is a fundamental parameter that describes the duration of one complete cycle of its voltage waveform. For AC voltage sources, it is inversely related to the frequency. While the period is less directly applicable to ideal DC voltage sources, ripple voltage in practical DC supplies exhibits periodic behavior. Understanding the period is critical for analyzing and designing circuits, particularly those containing reactive components, and for ensuring the proper operation of various electrical and electronic systems.
- The period (T) is the time for one complete cycle of a voltage waveform.
- For AC, T = 1/f, where f is the frequency.
- Reactive components (capacitors and inductors) have impedance that is frequency-dependent, therefore period-dependent.
- Ripple voltage in DC supplies also exhibits a period.
- Oscilloscopes and frequency counters are used to measure the period.